통계의 기대값과 표준 오차를 이해하기 위해 글을 작성하였습니다. 통계의 기본 개념 중에는 " 기대값"과 "표준 오차"가 있습니다. 이러한 개념은 데이터 변동성을 이해하고 통계 분석을 기반으로 정보에 입각한 의사 결정을 내리는 데 중요한 역할을 합니다.

이 글에서는 기대값과 표준 오차의 정의, 중요성, 계산 방법을 살펴보고, 실제 사례를 통해 그 실제적인 의미를 조명해 보겠습니다.
통계에서 기대값이란?
통계에서기대값이란? 무엇일까요?통계의 핵심에는 흔히 " 예상값"이라고도 하는 "기대값"이라는 개념이 있습니다. 기대값은 무작위 변수의 장기 평균 또는 평균을 나타냅니다. 기대값은 가능한 모든 결과와 관련 확률을 고려하여 특정 프로세스에서 평균적으로 얻을 수 있을 것으로 예상할 수 있는 것을 요약한 것입니다.
수학적으로, 가능한 값 x1 ,x2 ,…,xn 및 해당 확률 P(X=x1 ),P(X=x2 ),…,P(X=xn )을 갖는 이산 확률 변수 X에 대해 , 기대치 E(X)는 다음과 같이 계산됩니다.
E(X)=x1 ⋅P(X=x1 )+x2 ⋅P(X=x2 )+… +xn ⋅P(X=xn )
연속 확률 변수의 경우, 기대값은 가능한 값의 전체 범위에 대한 적분을 통해 계산됩니다.
예를 들어 주사위 굴리기를 생각해보세요.
가능한 결과는 1, 2, 3, 4, 5, 6이며, 각 결과는 다음과 같은 확률을 가집니다.
1/6. 주사위를 굴릴 때의 기대치는 다음과 같이 계산됩니다.
E(X)=1⋅61+2⋅61+3⋅61+4⋅61+5⋅61+6⋅61=3.5
통계학에서 표준 오차란?
기대값은 무작위 변수의 행동에 대한 중심 척도를 제공하는 반면, '표준 오차'는 모집단 매개변수의 추정과 관련된 변동성 또는 불확실성을 정량화합니다. 표본 데이터로 작업하여 더 큰 모집단에 대한 추론을 도출할 때 특히 중요합니다.
표준 오차는 기본적으로 표본 평균과 같은 표본 통계의 표준 편차입니다. 표준 오차는 표본 평균이 실제 모집단 평균에서 얼마나 벗어날 가능성이 있는지를 반영합니다. 표준 오차가 작을수록 모집단 매개변수의 추정치가 더 정확하다는 것을 나타냅니다.
표준 편차가 σ인 모집단의 n 관측치에서 계산된 표본 평균 xˉ의 경우 표준 오차 SE는 다음과 같이 계산됩니다.
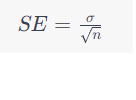
예시로 학생 점수를 평가한다고 하였을 때를 들겠습니다.
학생 100명으로 구성된 한 학급의 평균 시험 점수를 평가하는 시나리오를 생각해 보겠습니다. 학생 20명의 샘플을 무작위로 선택하고 이들의 평균 점수를 85점, 모집단 표준 편차 10으로 계산합니다. 표본 평균의 표준 오차는 다음과 같습니다.
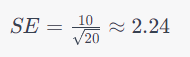
실무적 시사점 및 응용
A. 신뢰 구간
표준 오차는 신뢰 구간(실제 모집단 매개변수가 속할 가능성이 있는 범위)을 구성하는 데 중요한 역할을 합니다. 표본 크기가 크거나 표준 오차가 작을수록 신뢰 구간이 좁아져 추정의 정확도가 높아집니다.
B. 가설 검정
가설 검정에서 표준 오차는 Z-점수 또는 t-점수와 같은 검정 통계를 계산하는 데 사용되며, 이를 통해 표본과 모집단 매개변수 간에 관찰된 차이의 중요성을 평가할 수 있습니다.
C. 예측 모델링
표준 오차는 예측 모델의 신뢰성을 평가하는 데 도움이 됩니다. 표준 오차가 낮을수록 모델이 정확한 예측을 할 수 있는 능력이 있음을 나타냅니다.
결론
기대값과 표준 오차는 데이터를 이해하고, 의미 있는 결론을 도출하고, 불확실성을 정량화할 수 있도록 해주는 통계의 세계에서 중요한 개념입니다. 기대치는 프로세스의 평균 결과에 대한 인사이트를 제공하며, 표준 오차는 추정 및 예측의 정밀도를 정량화합니다. 통계학자, 연구자, 데이터 분석가는 이러한 개념과 계산을 숙달함으로써 데이터 변동성의 복잡성을 풀고 정보에 입각한 의사 결정을 내릴 수 있어 분석의 품질과 신뢰성을 높일 수 있습니다.
'기타' 카테고리의 다른 글
| 아웃룩 오류 해결하는 방법 3가지 (0) | 2023.11.09 |
|---|---|
| 통계학에서 표본 조사의 중요성, 종류, 장점 (0) | 2023.08.21 |
| 통계학에서 평균의 법칙에 대해 (0) | 2023.08.21 |
| 통계학에서 정규 분포와 Z점수 이해하기 (0) | 2023.08.21 |
| 통계학에서 확률이란 무엇인가 (0) | 2023.08.12 |

